決策樹 簡介
決策樹是最強大和最流行的分類和預測工具。決策樹是一種類似流程圖的樹結構,其中每個內部節點表示對屬性的測試,每個分支表示測試的結果,每個葉節點(終端節點)持有一個類標籤。
決策樹的構建: 可以通過基於屬性值測試將源集拆分為子集來“學習”樹。這個過程以稱為遞歸分區的遞歸方式在每個派生子集上重複。當節點處的子集都具有相同的目標變量值時,或者當拆分不再為預測增加值時,遞歸完成。決策樹分類器的構建不需要任何領域知識或參數設置,因此適用於探索性知識發現。決策樹可以處理高維資料。一般來說,決策樹分類器具有良好的準確性。決策樹歸納是學習分類知識的典型歸納方法。
決策樹表示:
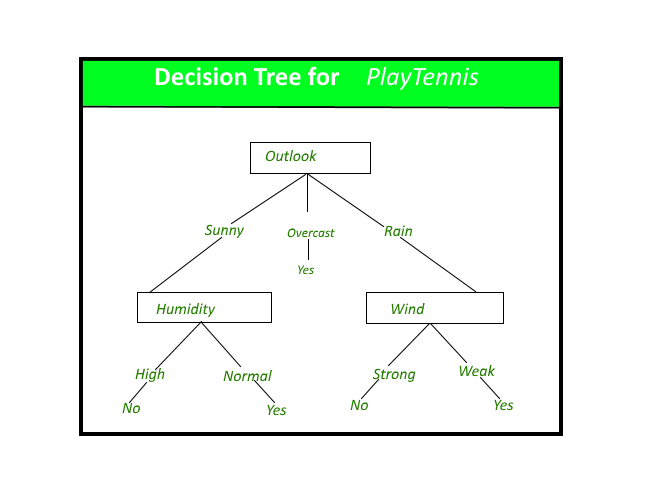
決策樹通過將實例從根到某個葉節點向下排序來對實例進行分類,這提供了實例的分類。一個實例的分類是從樹的根節點開始,測試該節點指定的屬性,然後向下移動對應屬性值的樹分支,如上圖所示。然後對以新節點為根的子樹重複此過程。
上圖中的決策樹根據是否適合打網球對特定的早晨進行分類,並返回與特定葉子關聯的分類。(在本例中為 Yes 或 No)。
例如,實例
(展望 = 晴天,溫度 = 炎熱,濕度 = 高,風 = 強)
將被排序到該決策樹的最左側分支,因此將被分類為否定實例。
換句話說,我們可以說決策樹代表了對實例屬性值的約束結合的析取。
(展望 = 晴天 ^ 濕度 = 正常) v (展望 = 陰天) v (展望 = 雨 ^ 風 = 弱)
基尼指數:
基尼指數是一個分數,用於評估分類組之間劃分的準確程度。基尼指數評估介於 0 和 1 之間的分數,其中 0 表示所有觀察值都屬於一個類,1 表示類內元素的隨機分佈。在這種情況下,我們希望基尼指數得分盡可能低。基尼指數是我們用來評估決策樹模型的評估指標。
執行:
#%%
from sklearn.datasets import make_classification
from sklearn import tree
from sklearn.model_selection import train_test_split
X, t = make_classification(100, 5, n_classes = 2, shuffle = True, random_state= 10)
X_train, X_test, t_train, t_test = train_test_split(X, t, test_size=0.3, shuffle = True, random_state=1)
#%%
model = tree.DecisionTreeClassifier()
model = model.fit(X_train, t_train)
#%%
predicted_value = model.predict(X_test)
print(predicted_value)
#%%
tree.plot_tree(model)
#%%
zeroes = 0
ones = 0
for i in range(0,len(t_train)):
if t_train[i] == 0:
zeroes +=1
else:
ones +=1
#%%
print(zeroes)
print(ones)
#%%
val = 1 - ((zeroes/70)*2 + (ones/70)*2)
print("Gini :",val)
match = 0
UnMatch = 0
for i in range(30):
if predicted_value[i] == t_test[i]:
match += 1
else:
UnMatch += 1
accuracy = match/30
print("Accuracy is: ",accuracy)
決策樹方法的優點和缺點 決策樹方法
的優點是:
- 決策樹能夠生成可理解的規則。
- 決策樹無需太多計算即可執行分類。
- 決策樹能夠處理連續變量和分類變量。
- 決策樹清楚地表明哪些字段對於預測或分類最重要。
決策樹方法的缺點:
- 決策樹不太適合目標是預測連續屬性值的估計任務。
- 決策樹在具有許多類和相對較少訓練示例的分類問題中容易出錯。
- 訓練決策樹的計算成本可能很高。生長決策樹的過程在計算上是昂貴的。在每個節點上,每個候選拆分字段必須在找到其最佳拆分之前進行排序。在某些算法中,使用了字段組合,並且必須搜索最佳組合權重。修剪算法也可能很昂貴,因為必須形成和比較許多候選子樹。
在下一篇文章中,我們將討論 JR Quinlan 給出的用於構建決策樹的 ID3 算法。
