ieee 754 二進位浮點數算術標準

Home >> Blog >> ieee 754 二進位浮點數算術標準

結束一天的SEO搜尋引擎優化工作後，又到了關心我們軟體工程業界標準規範的時間了。

ieee 754 二進位浮點數算術標準

IEEE 浮點算術標準 (IEEE 754) 是由電氣和電子工程師協會 (IEEE)於 1985 年制定的浮點計算技術標準。該標準解決了在各種浮點實現中發現的許多問題，這些問題使它們難以可靠地使用並降低了它們的可移植性。IEEE 標準 754 浮點是當今計算機上實數最常見的表示，包括基於 Intel 的 PC、Mac 和大多數 Unix 平台。

有幾種表示浮點數的方法，但 IEEE 754 在大多數情況下是最有效的。IEEE 754 有 3 個基本組成部分：

1. 尾數符號——
   就像名字一樣簡單。0 代表正數，1 代表負數。
2. 有偏指數——
   指數字段需要同時表示正指數和負指數。為了獲得存儲的指數，將偏差添加到實際指數。
3. 歸一化尾數 –
   尾數是科學計數法數字或浮點數的一部分，由其有效數字組成。這裡我們只有 2 位數字，即 O 和 1。因此，歸一化尾數是小數點左側只有一個 1 的尾數。

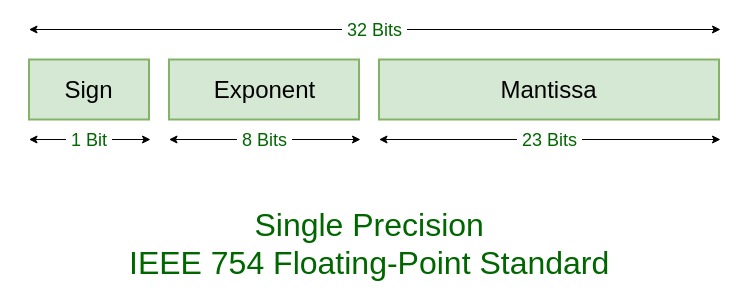
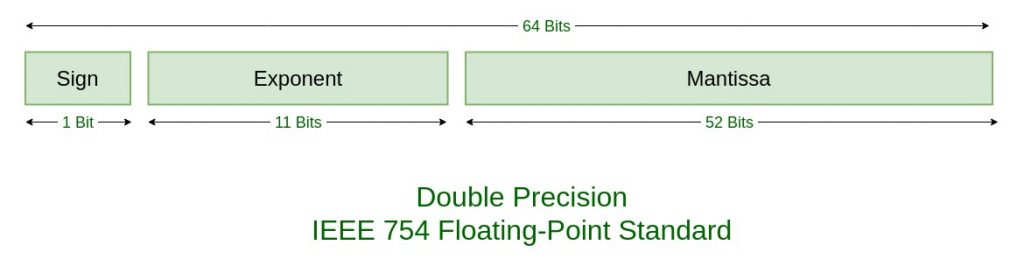
IEEE 754 數字根據以上三個分量分為兩種：單精度和雙精度。

例子 -

85.125
85 = 1010101
0.125 = 001
85.125 = 1010101.001
=1.010101001 x 2^6
符號 = 0

1、單精度：
有偏指數 127+6=133
133 = 10000101
歸一化尾數 = 010101001
我們將添加 0 來完成 23 位

IEEE 754 單精度為：
= 0 10000101 01010100100000000000000
這可以寫成十六進制形式42AA4000

2、雙精度：
有偏指數 1023+6=1029
1029 = 10000000101
歸一化尾數 = 010101001
我們將添加 0 來完成 52 位

IEEE 754 雙精度是：
= 0 10000000101 0101010010000000000000000000000000000000000000000000
這可以寫成十六進制形式4055480000000000

特殊值： IEEE 保留了一些可能不明確的值。

• 零 –
  零是一個特殊值，用指數和尾數 0 表示。-0 和 +0 是不同的值，儘管它們都是相等的。
• 非規範化 -
  如果指數全為零，但尾數不是，則該值是非規範化數字。這意味著該數字在二進制點之前沒有假定的前導數字。
• Infinity –
  值 +infinity 和 -infinity 用全 1 的指數和全 0 的尾數表示。符號位區分負無窮大和正無窮大。具有無限值的操作在 IEEE 中有很好的定義。
• 非數字 (NAN) –
  NAN 值用於表示錯誤值。這在指數字段全為 1 且符號位為零或尾數不是 1 後跟零時表示。這是一個特殊值，可用於表示尚未保存值的變量。

雙精度（僅將 255 替換為 2049）類似，浮點數範圍：

正浮點數的範圍可以分為規範化數字和僅使用分數精度的一部分的非規範化數字。由於每個浮點數都有一個對應的取反值，因此上述範圍圍繞零對稱。

到目前為止，有五個不同的數值範圍是單精度浮點數無法表示的：

1. 負數小於 – (2 – 2 -23 ) × 2 127（負溢出）
2. 大於 – 2 -149的負數（負下溢）
3. 零
4. 小於 2 -149的正數（正下溢）
5. 大於 (2 – 2 -23 ) × 2 127的正數（正溢出）

溢出通常意味著值變得太大而無法表示。下溢是一個不太嚴重的問題，因為它只是表示精度損失，保證接近於零。

有限 IEEE 浮點數的總有效範圍表如下所示：