Home >> Blog >> heap 資料結構簡介
heap 資料結構對於SEO搜尋引擎優化有直接幫助,讓我們一起來了解。
heap 資料結構簡介
heap是平衡二叉樹資料結構的一種特殊情況,其中根節點鍵與其子節點進行比較並進行相應排列。如果α有子節點β那麼 -
鍵(α)≥鍵(β)
由於 parent 的值大於 child 的值,因此該屬性生成Max Heap。基於這個標準,heap可以有兩種類型 -
For Input → 35 33 42 10 14 19 27 44 26 31
Min-Heap - 根節點的值小於或等於其任何一個子節點。
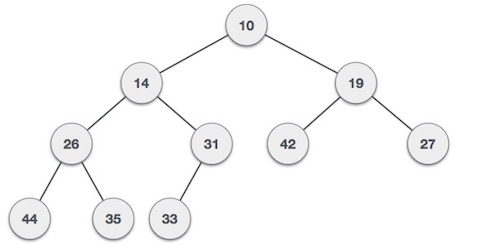
Max-Heap - 根節點的值大於或等於其任何一個子節點。
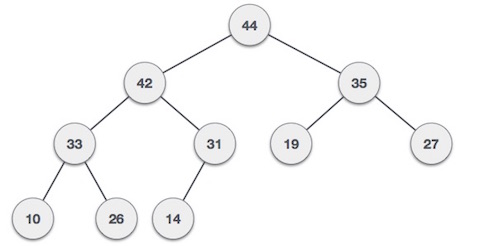
兩棵樹都是使用相同的輸入和到達順序構建的。
最大heap構建算法
我們將使用相同的範例來演示如何創建 Max Heap。創建最小heap的過程類似,但我們選擇最小值而不是最大值。
我們將通過一次插入一個元素來推導最大heap的算法。在任何時候,heap都必須保持其屬性。在插入時,我們還假設我們在已經heap積的樹中插入一個節點。
Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.
注- 在最小heap構造算法中,我們期望父節點的值小於子節點的值。
讓我們通過動畫插圖來了解 Max Heap 的構建。我們考慮之前使用的相同輸入樣本。

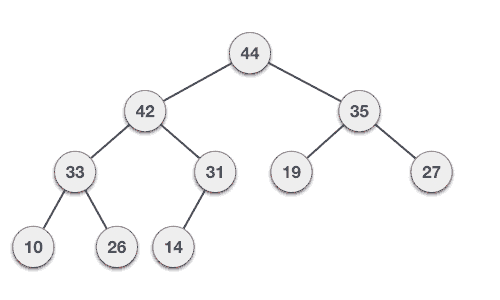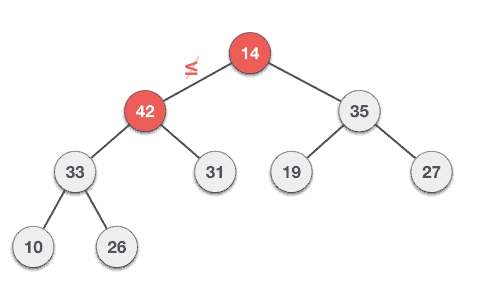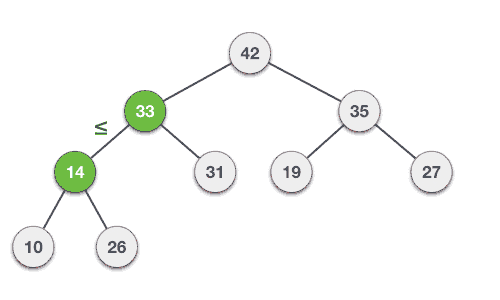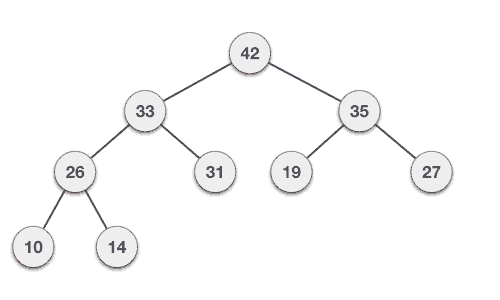
最大heap刪除算法
讓我們推導出一個從最大heap中刪除的算法。最大(或最小)heap中的刪除總是發生在根處以刪除最大(或最小)值。
Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.