cross entropy 機器學習交叉熵的簡要介紹

Home >> Blog >> cross entropy 機器學習交叉熵的簡要介紹

雲端計算，AI 學習以及機器學習是我們在執行完一整天的SEO search engine optimization 案子後，拿出來讓腦子休息的科技甜點。

不廢話，直接跳到今日的主題 cross entropy

cross entropy 機器學習交叉熵的簡要介紹

交叉熵通常用作機器學習中的損失函數。

交叉熵是資訊論領域的一種度量，建立在熵的基礎上，通常計算兩個概率分佈之間的差異。它與計算兩個概率分佈之間的相對熵的KL散度密切相關但又有所不同，而交叉熵可以被認為是計算分佈之間的總熵。

交叉熵也與邏輯損失相關並且經常與邏輯損失混淆，稱為對數損失。儘管這兩個度量來自不同的來源，但當用作分類模型的損失函數時，兩個度量計算相同的數量並且可以互換使用。

在本教學中，您將發現機器學習的交叉熵。

完成本教學後，您將了解：

• 如何從頭開始計算交叉熵並使用標準機器學習庫。
• 在優化邏輯回歸和人工神經網絡等分類模型時，交叉熵可以用作損失函數。
• 交叉熵不同於 KL 散度，但可以使用 KL 散度計算，並且不同於對數損失，但在用作損失函數時計算相同的量。

從市場上的新書《機器學習概率論》開始您的項目，包括分步教學和所有示例的Python 源程式碼文件。

讓我們開始吧。

• 2019 年 10 月更新：給出了相同分佈的交叉熵示例並更新了此案例的描述（感謝 Ron U）。添加了計算已知類標籤熵的示例。
• 2019 年 11 月更新：改進了結構並添加了對熵的更多解釋。增加了對預測類別概率的直覺。
• 2020 年 12 月更新：調整了對資訊和熵的介紹，使其更加清晰。

教學概述

本教學分為五個部分；他們是：

1. 什麼是交叉熵？
2. 交叉熵與 KL 散度
3. 如何計算交叉熵

   1.兩個離散概率分佈

   2.計算分佈之間的交叉熵

   3.計算分佈與其自身之間的交叉熵

   4.使用 KL 散度計算交叉熵

4. 交叉熵作為損失函數

   1.計算類標籤的熵

   2.計算類標籤和概率之間的交叉熵

   3.使用 Keras 計算交叉熵

   4.對預測概率的交叉熵的直覺

5. 交叉熵與對數損失

   對數損失是負對數似然

   對數損失和交叉熵計算相同的東西

什麼是交叉熵？

交叉熵是對給定隨機變量或事件集的兩個概率分佈之間差異的度量。

您可能還記得，資訊量化了編碼和傳輸事件所需的位數。低概率事件有更多資訊，高概率事件有更少資訊。

在資訊論中，我們喜歡描述一個事件的“驚喜”。一個事件越不可能越令人驚訝，這意味著它包含更多資訊。

• Low Probability Event (surprising): More information.
• 較高概率事件（不足為奇）：資訊較少。

給定事件P(x)的概率，可以計算事件x的資訊h(x ) ，如下所示：

• h(x) = -log(P(x))

熵是傳輸從概率分佈中隨機選擇的事件所需的比特數。偏態分佈具有較低的熵，而事件具有相等概率的分佈具有較大的熵。

偏斜的概率分佈具有較少的“驚喜”，反過來又具有低熵，因為可能的事件占主導地位。平衡分佈更令人驚訝，並且熵更高，因為事件發生的可能性相同。

• 偏態概率分佈（不足為奇）：低熵。
• 平衡概率分佈（令人驚訝）：高熵。

熵H(x)可以針對具有X個離散狀態中的一組x的隨機變量和它們的概率P(x)計算如下：

• H(X) = – XP(x) 中 x 的總和 * log(P(x))

如果您想了解有關計算事件資訊和分佈熵的更多資訊，請參閱本教學：

• 資訊熵簡介

交叉熵建立在資訊論中的熵的概念之上，併計算與另一種分佈相比，從一個分佈表示或傳輸平均事件所需的比特數。

交叉熵是當我們使用模型 q 時，對來自分佈為 p 的源的數據進行編碼所需的平均位數…

第 57 頁，機器學習：概率視角，2012 年。

如果我們考慮目標或潛在概率分佈 P 和目標分佈 Q 的近似值，則該定義的直覺出現，那麼來自 P 的 Q 的交叉熵是使用 Q 而不是 P 表示事件的附加比特數。

兩個概率分佈之間的交叉熵，例如 P 中的 Q，可以正式表示為：

• 高（P，Q）

其中H()是交叉熵函數，P可能是目標分佈，Q是目標分佈的近似值。

可以使用來自 P 和 Q 的事件的概率來計算交叉熵，如下所示：

• (P, Q) = – XP(x) 中 x 的總和 * log(Q(x))

其中 P(x) 是事件 x 在 P 中的概率，Q(x) 是事件 x 在 Q 中的概率，log 是以 2 為底的對數，這意味著結果以位為單位。如果改為使用以 e 為底的或自然對數，則結果將具有稱為 nats 的單位。

此計算適用於離散概率分佈，儘管類似的計算可用於使用跨事件的積分而不是總和的連續概率分佈。

結果將是一個以比特為單位的正數，如果兩個概率分佈相同，則結果將等於分佈的熵。

注意：這個符號看起來很像聯合概率，或者更具體地說，是 P 和 Q 之間的聯合熵。這是誤導性的，因為我們正在用交叉熵對概率分佈之間的差異進行評分。然而，聯合熵是一個不同的概念，它使用相同的符號，而是計算兩個（或更多）隨機變量的不確定性。

交叉熵與 KL 散度

交叉熵不是 KL Divergence。

交叉熵與散度度量有關，例如Kullback-Leibler 或 KL，散度量化一個分佈與另一個分佈的差異程度。

具體來說，KL 散度測量的量與交叉熵非常相似。它測量用 Q 而不是 P 表示消息所需的平均額外位數，而不是總位數。

"換句話說，KL 散度是編碼數據所需的額外比特的平均數量，因為我們使用分佈 q 來編碼數據而不是真實分佈 p。"

第 58 頁，Machine Learning: A Probabilistic Perspective, 2012.

因此，KL 散度通常被稱為“相對熵”。

• 交叉熵：表示來自 Q 而不是 P 的事件的平均總比特數。
• 相對熵( KL Divergence )：表示來自 Q 而不是 P 的事件的平均額外比特數。

KL 散度可以計算為 P 中每個事件的概率的負總和，乘以 Q 中事件的概率與 P 中事件的概率的對數。通常，log base-2 以便結果以位。

• KL(P || Q) = – XP(x) 中 x 的總和 * log(Q(x) / P(x))

總和中的值是給定事件的散度。

因此，我們可以通過將分佈的熵加上由 KL 散度計算的附加熵來計算交叉熵。鑑於兩種計算的定義，這是直觀的；例如：

• H(P, Q) = H(P) + KL(P || Q)

其中 H(P, Q) 是 Q 與 P 的交叉熵，H(P) 是 P 的熵，KL(P || Q) 是 Q 與 P 的散度。

可以將概率分佈的熵計算為每個事件的概率的負和乘以事件的概率的對數，其中對數以 2 為底，以確保結果以位為單位。

• H(P) = – X 上的總和 x p(x) * log(p(x))

與 KL 散度一樣，交叉熵也不是對稱的，這意味著：

• H(P, Q) != H(Q, P)

正如我們稍後將看到的，當將交叉熵和 KL 散度用作優化分類預測模型的損失函數時，它們都會計算相同的數量。正是在這種情況下，您有時可能會看到交叉熵和 KL 散度是相同的。

有關 KL Divergence 的更多詳細資訊，請參閱教學：

• 如何計算機器學習的 KL 散度

如何計算交叉熵

在本節中，我們將通過一個小例子來具體計算交叉熵。

兩個離散概率分佈

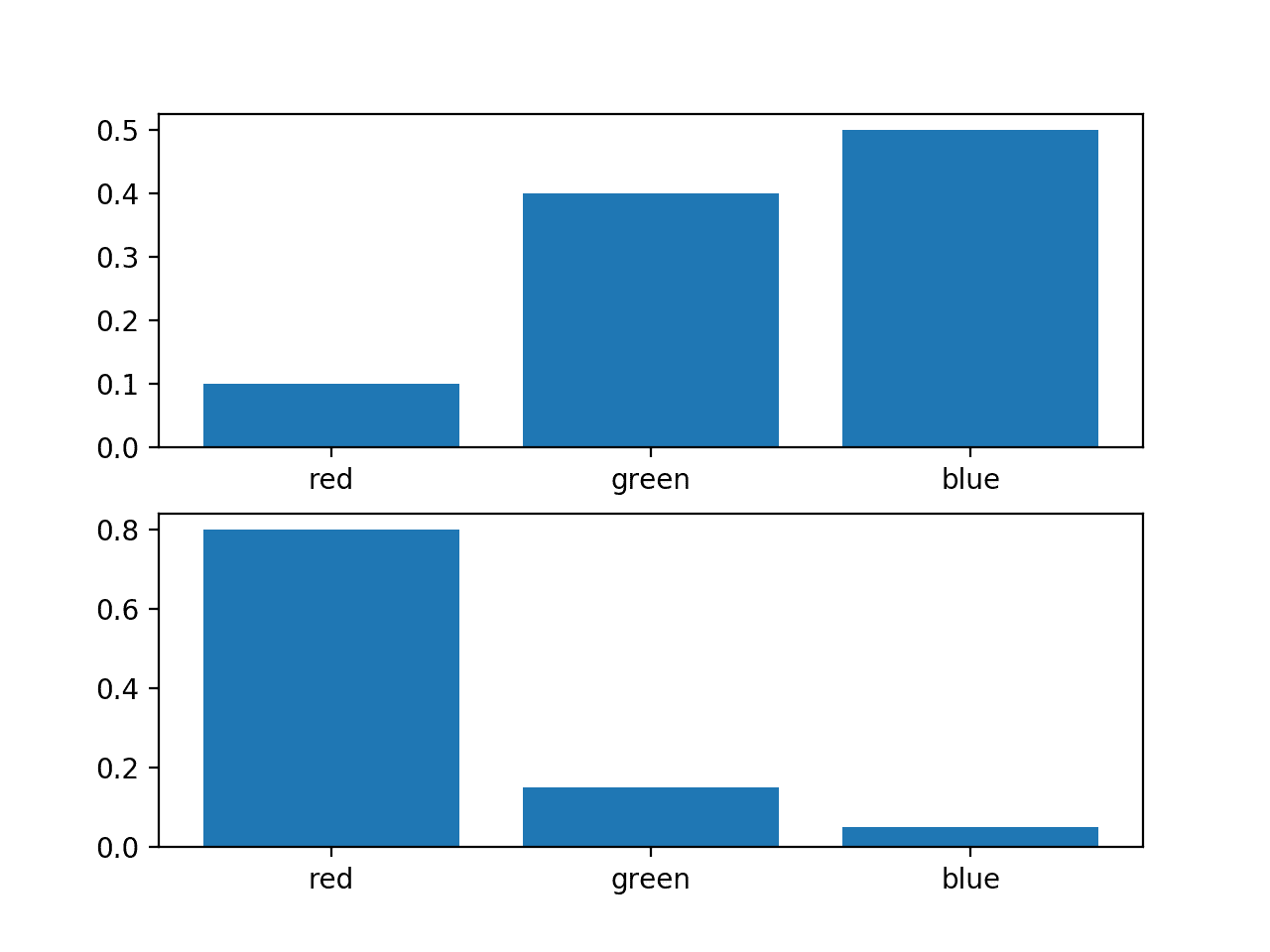
考慮一個隨機變量，其中三個離散事件為不同顏色：紅色、綠色和藍色。

對於這個變量，我們可能有兩種不同的概率分佈；例如：

我們可以繪製這些概率的條形圖，以將它們直接作為概率直方圖進行比較。

下面列出了完整的示例。

運行該示例會為每個概率分佈創建一個直方圖，從而可以直接比較每個事件的概率。

我們可以看到確實分佈不同。

計算分佈之間的交叉熵

接下來，我們可以開發一個函數來計算兩個分佈之間的交叉熵。

我們將使用 log base-2 來確保結果以位為單位。

然後我們可以使用這個函數從 Q 計算 P 的交叉熵，以及從 P 計算相反的 Q。

將所有這些結合在一起，下面列出了完整的示例。

運行該示例首先從 P 計算 Q 的交叉熵剛好超過 3 位，然後從 Q 計算 P 的交叉熵剛好低於 3 位。

計算分佈與其自身之間的交叉熵

如果兩個概率分佈相同，那麼它們之間的交叉熵就是分佈的熵。

我們可以通過計算 P 與 P 和 Q 與 Q 的交叉熵來證明這一點。

下面列出了完整的示例。

運行該示例首先計算 Q 與 Q 的交叉熵，其計算為 Q 的熵，以及 P 與 P 的交叉熵，計算為 P 的熵。

使用 KL 散度計算交叉熵

我們還可以使用 KL 散度計算交叉熵。

使用 KL 散度計算的交叉熵應該是相同的，計算分佈之間的 KL 散度可能會很有趣，以查看相對熵或所需的額外比特，而不是由交叉熵計算的總比特。

首先，我們可以定義一個函數來使用 log base-2 計算分佈之間的 KL 散度，以確保結果也以位為單位。

為了使示例簡單，我們可以將 H(P, Q) 的交叉熵與 KL 散度 KL(P || Q) 和熵 H(P) 進行比較。

下面列出了完整的示例。

交叉熵作為損失函數

在優化分類模型時，交叉熵被廣泛用作損失函數。

您可能遇到的兩個示例包括邏輯回歸算法（一種線性分類算法）和可用於分類任務的人工神經網絡。

使用交叉熵誤差函數而不是平方和來解決分類問題可以加快訓練速度並提高泛化能力。

— 第 235 頁，模式識別和機器學習，2006 年。

分類問題是那些涉及一個或多個輸入變量和類別標籤預測的問題

輸出變量只有兩個標籤的分類任務稱為二元分類問題，而具有兩個以上標籤的問題稱為分類或多類分類問題。

• 二元分類：預測給定示例的兩個類標籤之一的任務。
• 多類分類：預測給定示例的兩個以上類標籤之一的任務。

我們可以看到，交叉熵的思想可能對優化分類模型很有用。

每個示例都有一個已知的類標籤，概率為 1.0，所有其他標籤的概率為 0.0。模型可以估計示例屬於每個類別標籤的概率。然後可以使用交叉熵來計算兩個概率分佈之間的差異。

因此，我們可以將一個示例的分類映射到具有如下概率分佈的隨機變量的概念上：

• 隨機變量：我們需要預測類標籤的示例。
• 事件：可以預測的每個類標籤。

在分類任務中，我們知道輸入的目標概率分佈 P 作為類標籤 0 或 1，分別解釋為“不可能”或“確定”的概率。這些概率一點也不奇怪，因此它們沒有資訊內容或零熵。

我們的模型試圖近似目標概率分佈 Q。

在分類語言中，這些是實際概率和預測概率，或y和yhat。

• 預期概率( y )：數據集中 (P) 中示例的每個類標籤的已知概率。
• 預測概率( yhat )：模型預測的每個類別標籤的概率 (Q)。

因此，我們可以使用上述交叉熵計算來估計單個預測的交叉熵；例如。

• H(P, Q) = – XP(x) 中 x 的總和 * log(Q(x))

每個地方x in X is a class label that could be assigned to the example, and P(x) will be 1 for the known label and 0 for all other labels.

二進制分類任務中單個示例的交叉熵可以通過展開求和運算來表示，如下所示：

• H(P, Q) = – (P(class0) * log(Q(class0)) + P(class1) * log(Q(class1)))

您可能會在教科書中看到這種計算交叉熵的形式。

如果只有兩個類標籤，則概率被建模為正類標籤的伯努利分佈。這意味著第 1 類的概率由模型直接預測，第 0 類的概率為 1 減去預測概率，例如：

• 預測 P(class0) = 1 – yhat
• 預測 P(class1) = yhat

在計算分類任務的交叉熵時，使用以 e 為底的或自然對數。這意味著單位是 nat，而不是位。

我們經常對最小化整個訓練數據集中模型的交叉熵感興趣。這是通過計算所有訓練示例的平均交叉熵來計算的。

計算類標籤的熵

回想一下，當兩個分佈相同時，它們之間的交叉熵等於概率分佈的熵。

在為分類任務準備數據時，使用值 0 和 1 對類標籤進行編碼。

例如，如果一個分類問題具有三個類別，並且一個示例具有第一類的標籤，則概率分佈將為 [1, 0, 0]。如果一個示例具有第二類的標籤，它將具有兩個事件的概率分佈為 [0, 1, 0]。這稱為單熱編碼。

這個概率分佈沒有任何資訊，因為結果是確定的。我們知道班級。因此，該變量的熵為零。

這是一個重要的概念，我們可以通過一個工作示例來演示它。

假設有 3 個類別的分類問題，我們有一個屬於每個類別的示例。我們可以將每個示例表示為離散概率分佈，該示例所屬類別的概率為 1.0，所有其他類別的概率為 0.0。

我們可以計算“事件”中每個“變量”的概率分佈的熵。

下面列出了完整的示例。

我們可以看到，在每種情況下，熵都是 0.0（實際上是一個非常接近於零的數字）。

請注意，我們必須在 0.0 值中添加一個非常小的值以避免log()爆炸，因為我們無法計算 0.0 的 log。

因此，已知類標籤的熵始終為 0.0。

這意味著對於類標籤具有相同概率分佈的兩個分佈（真實分佈和預測分佈）的交叉熵也將始終為 0.0。

回想一下，在訓練數據集上使用交叉熵評估模型時，我們對數據集中所有示例的交叉熵進行平均。

因此，訓練模型時的交叉熵為 0.0 表明預測的類概率與訓練數據集中的概率相同，例如零損失。

我們可以很容易地將 KL 散度作為損失函數而不是交叉熵來最小化。

回想一下，KL 散度是傳輸一個變量與另一個變量相比所需的額外比特。它是沒有類標籤熵的交叉熵，我們知道它無論如何都會為零。

因此，最小化 KL 散度和分類任務的交叉熵是相同的。

最小化這種 KL 散度正好對應於最小化分佈之間的交叉熵。

在實踐中，0.0 的交叉熵損失通常表明該模型已經過擬合了訓練數據集，但這是另一回事。

計算類標籤和概率之間的交叉熵

使用交叉熵進行分類通常會根據類的數量給出不同的具體名稱，反映了分類任務的名稱；例如：

• Binary Cross-Entropy：交叉熵作為二元分類任務的損失函數。
• Categorical Cross-Entropy：交叉熵作為多類分類任務的損失函數。

我們可以通過一個工作示例來使用交叉熵作為損失函數。

考慮一個具有以下 10 個實際類標籤 (P) 和預測類標籤 (Q) 的二類分類任務。

對於每個實際概率和預測概率，我們必須將預測轉換為每個事件的概率分佈，在這種情況下，類 {0, 1} 為 1 減去類 0 的概率和類 1 的概率。

然後我們可以計算交叉熵並對所有示例重複該過程。

最後，我們可以計算整個數據集的平均交叉熵，並將其報告為模型在數據集上的交叉熵損失。

將所有這些結合在一起，下面列出了完整的示例。

報告了所有示例的最終平均交叉熵損失，在這種情況下，為 0.247 nats。

這就是在交叉熵損失函數下優化邏輯回歸模型或神經網絡模型時計算交叉熵損失的方式。

使用 Keras 計算交叉熵

我們可以通過使用Keras 深度學習 API中的binary_crossentropy()函數來計算我們的小數據集的交叉熵損失來確認相同的計算。

下面列出了完整的示例。

注意：此示例假設您已安裝Keras 庫（例如 2.3 或更高版本）並配置了後端庫，例如TensorFlow（2.0 或更高版本）。如果沒有，您可以跳過運行此示例。

運行該示例，我們可以看到報告的相同平均交叉熵損失為 0.247 nats。

這證實了交叉熵的正確手動計算。

1 Average Cross Entropy: 0.247 nats

對預測概率的交叉熵的直覺

我們可以進一步發展預測類別概率的交叉熵的直覺。

例如，假設平均交叉熵損失為 0.0 是一個完美模型，那麼大於零的平均交叉熵值究竟意味著什麼？

我們可以探索這個問題，而不是類標籤為 0 和 1 的二元分類問題。這是一個離散概率分佈，其中包含兩個事件，一個事件具有一定概率，另一個事件具有不可能的概率。

然後，我們可以計算從目標分佈的完美匹配到完全相反的概率分佈的不同“預測”概率分佈的交叉熵。

我們預計，隨著預測的概率分佈與目標分佈的進一步偏離，計算的交叉熵將增加。

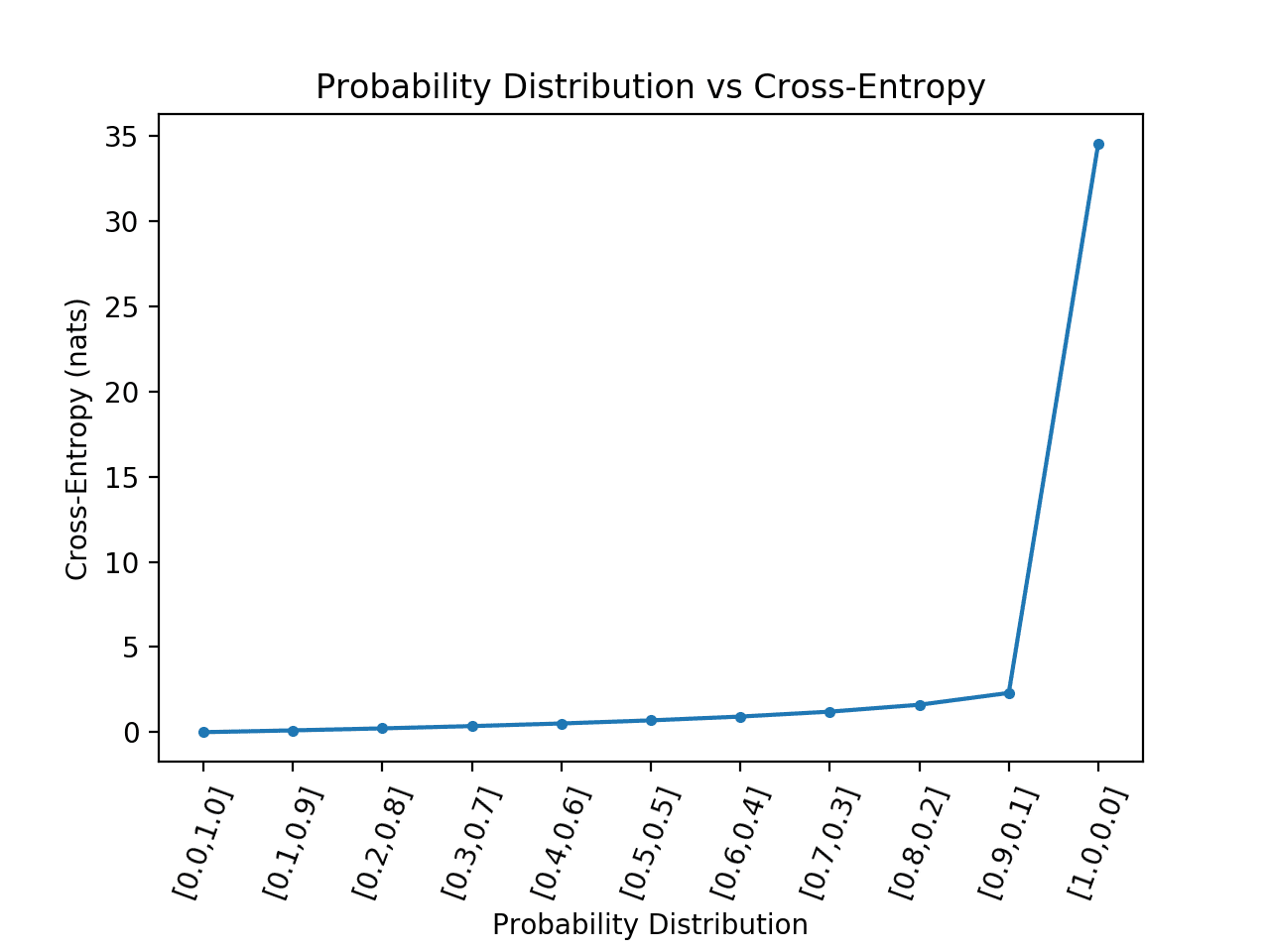
下面的示例實現了這一點，並繪製了預測概率分佈的交叉熵結果與兩個事件的目標 [0, 1] 相比，正如我們在二元分類任務中看到的交叉熵一樣。

運行該示例計算每個概率分佈的交叉熵分數，然後將結果繪製為線圖。

我們可以看到，正如預期的那樣，當預測概率分佈與目標分佈匹配時，交叉熵從 0.0（最左邊的點）開始，然後隨著預測概率分佈的發散而穩步增加。

當預測的概率分佈與目標分佈完全相反時，我們還可以看到交叉熵的巨大飛躍，即 [1, 0] 與 [0, 1] 的目標相比.

我們不會有一個模型來預測二進制分類任務中所有情況的完全相反的概率分佈。

因此，我們可以刪除這種情況並重新計算繪圖

下面列出了程式碼的更新版本。

運行該示例可以更好地了解概率分佈的散度與計算的交叉熵之間的關係。

我們可以看到一個超線性關係，預測的概率分佈越偏離目標，交叉熵的增加就越大。

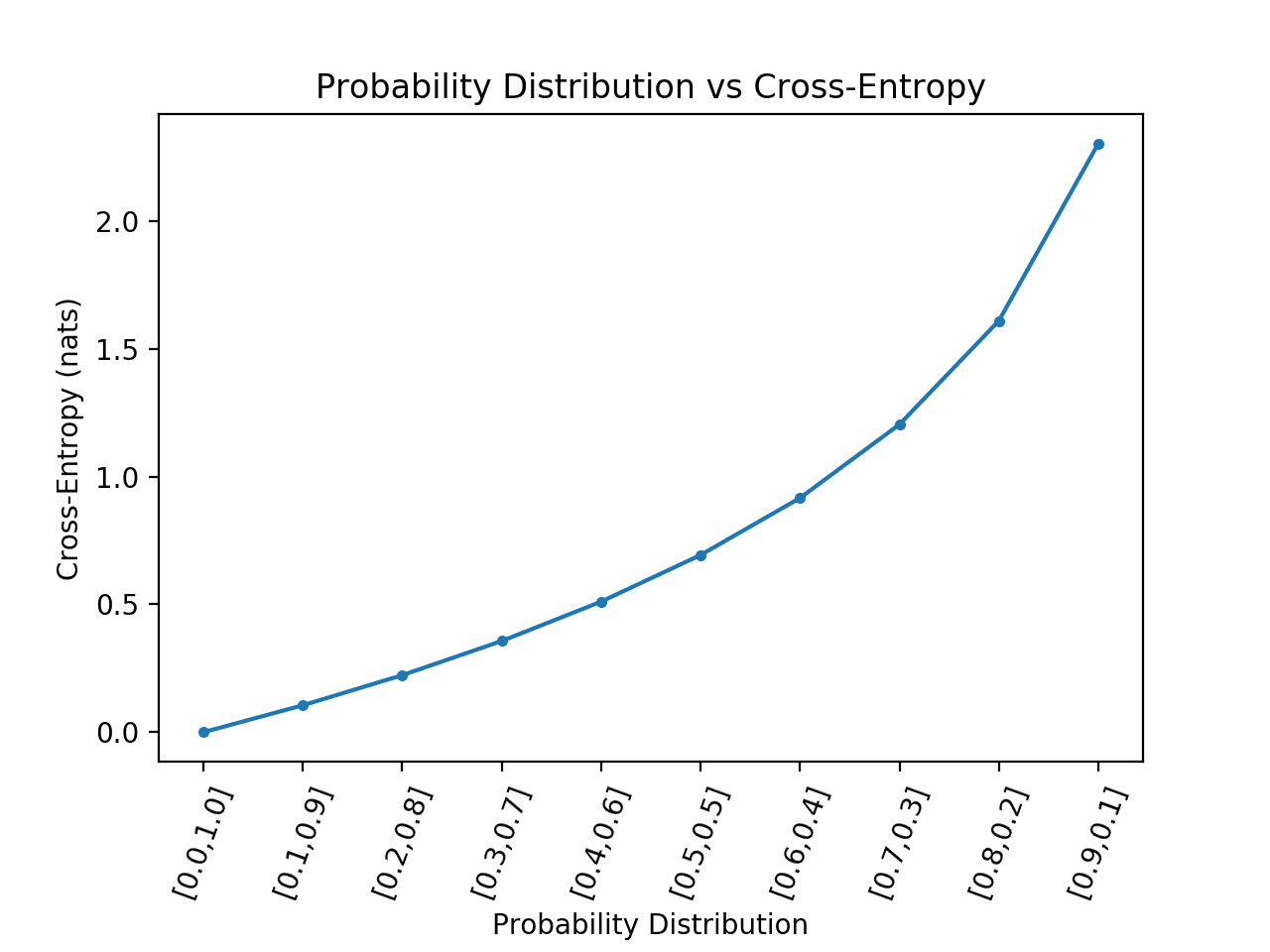
像這樣的圖可以用作解釋為二進制分類數據集的模型報告的平均交叉熵的指南。

例如，您可以使用這些交叉熵值來解釋 Keras 為二進制分類任務上的神經網絡模型或使用 logloss 度量評估的 scikit-learn 中的二進制分類模型報告的平均交叉熵。

您可以使用它來回答一般問題：

如果您在 nats 中工作（通常是這樣）並且平均交叉熵小於 0.2，那麼您的開端良好，小於 0.1 或 0.05 會更好。

另一方面，如果你得到的平均交叉熵大於 0.2 或 0.3，你可能會有所改進，如果你得到的平均交叉熵大於 1.0，那麼你正在做一些糟糕的概率預測在您的數據集中的許多示例上。

我們可以將這些關於平均交叉熵的直覺總結如下：

• 交叉熵 = 0.00：完美概率。
• 交叉熵 < 0.02：很大的概率。
• 交叉熵 < 0.05：在正確的軌道上。
• 交叉熵 < 0.20：很好。
• 交叉熵 > 0.30：不太好。
• 交叉熵 > 1.00：很糟糕。
• 交叉熵 > 2.00有些東西壞了。

在解釋邏輯回歸模型或人工神經網絡模型的交叉熵（對數損失）時，此列表將提供有用的指導。

您還可以計算每個班級的單獨平均交叉熵分數，並幫助梳理出您所建模的哪些班級具有良好的概率，哪些班級可能會搞砸。

交叉熵與對數損失

交叉熵不是對數損失，但它們在用作分類問題的損失函數時計算相同的數量。

對數損失是負對數似然

邏輯損失是指通常用於優化邏輯回歸模型的損失函數。

它也可能被稱為對數損失（令人困惑）或簡稱為對數損失。

許多模型在稱為最大似然估計或 MLE 的概率框架下進行了優化，該框架涉及找到一組最能解釋觀察到的數據的參數。

這涉及選擇一個似然函數，該函數定義一組觀察（數據）被給予模型參數的可能性。當使用對數似然函數（這很常見）時，它通常被稱為優化模型的對數似然。因為在實踐中最小化一個函數比最大化它更常見，所以通過在前面添加一個負號來反轉對數似然函數。這將其轉換為負對數似然函數或簡稱 NLL。

在伯努利概率分佈函數（兩類）最大似然估計框架下推導對數似然函數，計算結果為：

. 負對數似然(P, Q) = -(P(class0) * log(Q(class0)) + P(class1) * log(Q(class1)))

通過計算似然函數對數的平均值，可以在所有訓練示例上平均該數量。

二元分類問題的負對數似然通常簡稱為“對數損失”，作為邏輯回歸的損失函數。

.對數損失 = 負對數似然，在伯努利概率分佈下

我們可以看到，負對數似然與用於伯努利概率分佈函數（兩個事件或類別）的交叉熵的計算相同。事實上，Multinoulli 分佈（多類分類）的負對數似然也與交叉熵的計算相匹配。

有關日誌丟失和負對數似然的更多資訊，請參閱教學：

. 帶有最大似然估計的 Logistic 回歸的簡要介紹

對數損失和交叉熵計算相同的東西

對於分類問題，“ log loss ”、“ cross-entropy ”和“ negative log-likelihood ”可以互換使用。

更一般地，術語“交叉熵”和“負對數似然”在分類模型的損失函數的上下文中可以互換使用。

邏輯回歸的負對數似然由 [...] 給出，這也稱為交叉熵誤差函數。

機器學習：概率視角，2012 年。

因此，計算對數損失將給出與計算伯努利概率分佈的交叉熵相同的數量。我們可以通過使用scikit-learn API中的log_loss() 函數計算日誌損失來確認這一點。

計算上一節中同一組實際概率和預測概率的平均對數損失應該得到與計算平均交叉熵相同的結果。

下面列出了完整的示例。

1 Average Log Loss: 0.247

這並不意味著對數損失計算交叉熵或交叉熵計算對數損失。

相反，它們是不同的量，來自不同的研究領域，在為分類任務計算損失函數的條件下，會產生等效的計算和結果。具體來說，交叉熵損失函數等價於伯努利或多努利概率分佈下的最大似然函數。

這證明了最大似然估計的研究與離散概率分佈的資訊論之間的聯繫。

它不僅限於離散概率分佈，這一事實令許多第一次聽到它的從業者感到驚訝。

具體來說，在最大似然估計框架下優化的線性回歸假設目標變量的高斯連續概率分佈，並涉及最小化均方誤差函數。這相當於具有高斯概率分佈的隨機變量的交叉熵。

任何由負對數似然組成的損失都是訓練集定義的經驗分佈和模型定義的概率分佈之間的交叉熵。例如，均方誤差是經驗分佈和高斯模型之間的交叉熵。

有點令人震驚，來自連續隨機變量的微分熵領域。

這意味著如果您計算覆蓋相同事件（具有相同的均值和標準差）的兩個高斯隨機變量之間的均方誤差，那麼您正在計算變量之間的交叉熵。

這也意味著，如果您使用均方誤差損失來優化回歸問題的神經網絡模型，那麼您實際上是在使用交叉熵損失。