Home >> Blog >> BFS 圖像廣度優先搜尋
今天的內容不談我們最熟悉的SEO搜尋引擎優化,我們來談談 BFS 圖像廣度優先搜尋。
BFS 圖像廣度優先搜尋
BFS 圖像廣度優先搜尋類似於樹的廣度優先搜尋。這裡唯一的問題是,與樹不同,圖可能包含循環,因此我們可能會再次來到同一個節點。為了避免多次處理一個節點,我們使用一個布爾訪問數組。為簡單起見,假設所有頂點都可以從起始頂點到達。BFS 使用隊列數據結構進行搜尋。
例如,在下圖中,我們從頂點 2 開始搜尋。當我們到達頂點 0 時,我們尋找它的所有相鄰頂點。2也是0的相鄰頂點。如果我們不標記訪問過的頂點,那麼2將被再次處理,它將成為一個非終止進程。
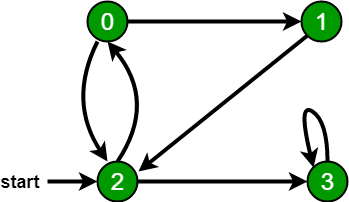
一個圖可以有多個 BFS 搜尋。上圖的不同 BFS 搜尋:
2, 3, 0, 1
2, 0, 3, 1
以下是來自給定源的簡單廣度優先搜尋的實現。
該實現使用圖的鄰接表表示。STL的列表容器存儲相鄰節點列表和 BFS 搜尋所需的節點隊列。
// Program to print BFS traversal from a given
// source vertex. BFS( int s) traverses vertices
// reachable from s.
# include< bits/stdc++. h>
using namespace std;
// This class represents a directed graph using
// adjacency list representation
class Graph
{
int V; // No. of vertices
// Pointer to an array containing adjacency
// lists
vector< list< int>> adj ;
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int v, int w);
// prints BFS traversal from a given source s
void BFS( int s);
};
Graph:: Graph( int V)
{
this->V = V;
adj.resize(V);
}
void Graph::addEdge(int v, int w)
{
adj[v]. push_back(w); // Add w to v’s list.
}
void Graph:: BFS(int s)
{
// Mark all the vertices as not visited
vector< bool> visited;
visited. resize(V,false);
// Create a queue for BFS
list< int> queue;
// Mark the current node as visited and enqueue it
visited[ s] = true;
queue. push_back(s);
while(! queue.empty())
{
// Dequeue a vertex from queue and print it
s = queue.front();
cout << s << " ";
queue.pop_front();
// Get all adjacent vertices of the dequeued
// vertex s. If a adjacent has not been visited,
// then mark it visited and enqueue it
for (auto adjecent: adj[s])
{
if (!visited[ adjecent])
{
visited[ adjecent] = true;
queue.push_ back(adjecent);
}
}
}
}
// Driver program to test methods of graph class
int main()
{
// Create a graph given in the above diagram
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "Following is Breadth First Traversal "
<< "(starting from vertex 2) \ n";
g.BFS(2);
return 0;
}
輸出
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1
時間複雜度: O(V+E),其中 V 是節點數,E 是邊數。
輔助空間: O(V)
插圖 :
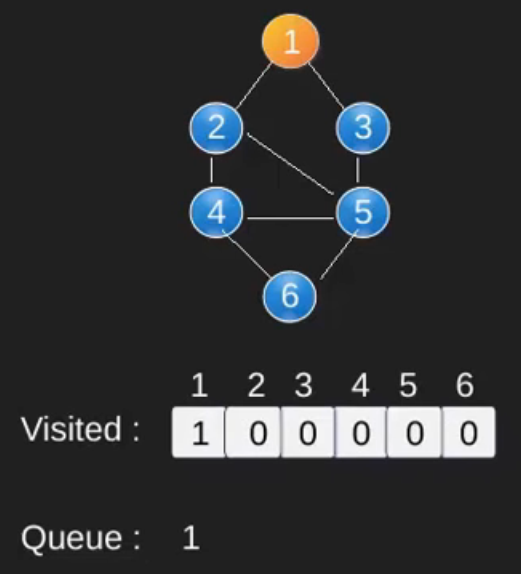
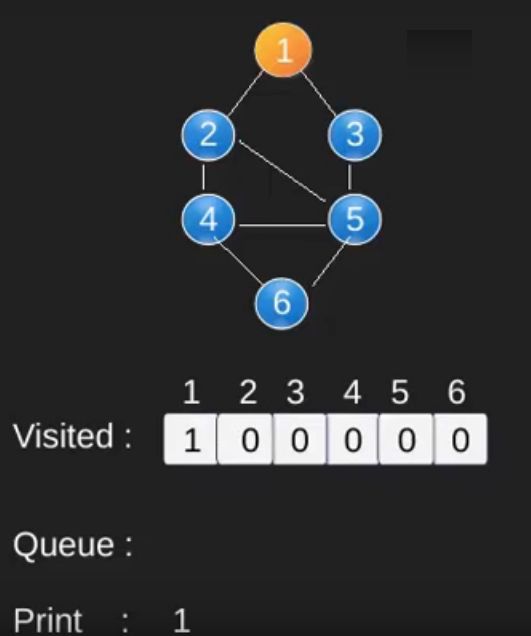
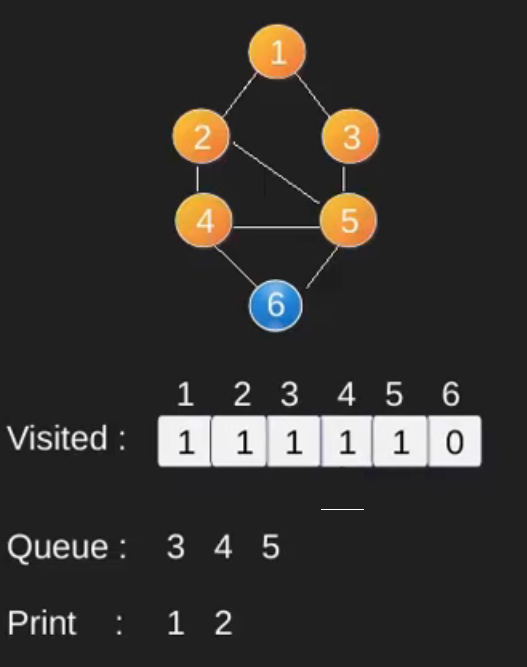
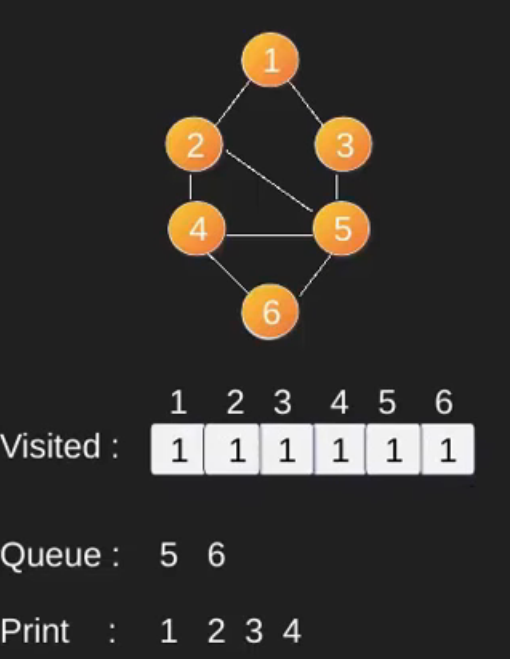
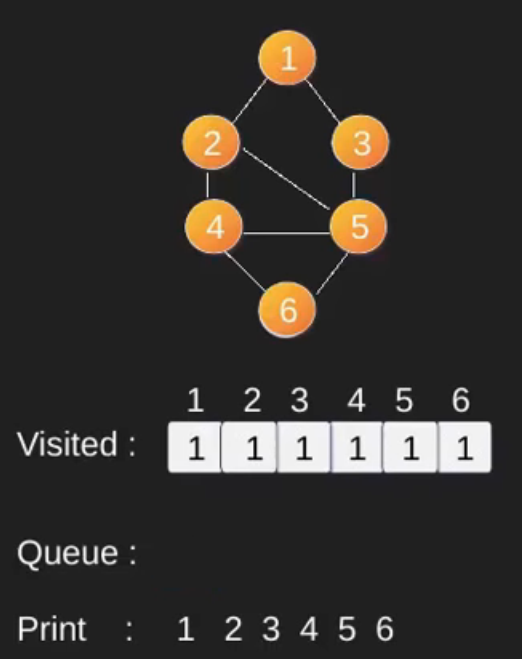
請注意,上面的程式碼僅搜尋從給定源頂點可到達的頂點。頂點可能無法從給定頂點(例如斷開連接圖)到達。
要列印所有頂點,我們可以修改 BFS 函數,從所有節點開始一個一個地搜尋(就像DFS 修改版一樣)。
BFS 搜尋整個圖的 C++ 程式碼(對有向圖和無向圖都有效),可能有多個斷開的組件,如下所示:
/*******************************************************
* Generic Function for BFS traversal of a Graph
* (valid for directed as well as undirected graphs
* which can have multiple disconnected commponents)
*
********** Inputs *************************************
* V - represents number of vertices in the Graph
* adj[] - represents adjacency list for the Graph
*
********** Output *************************************
* bfs_traversal - a vector containing bfs traversal
* for entire graph
*******************************************************/
vector< int> bfsOfGraph(int V, vector< int> adj[])
{
vector< int> bfs_traversal;
vector< bool> vis(V, false);
for ( int i = 0; i < V; + +i) {
if (!vis[i]) {
queue< int> q;
vis[i] = true;
q.push(i);
while (!q. empty()) {
int g_node = q.front();
q.pop();
bfs _traversal.push_back(g_node);
for (auto it : adj[g_node]) {
if (! vis[ it]) {
vis[ it] = true;
q. push(it);
}
}
}
}
}
return bfs_traversal;
}
