radix sort 理解基數排序方法

Home >> Blog >> radix sort 理解基數排序方法

平常執行SEO優化案子之餘，是否也會想讓自己的工程師腦子稍微轉換一下內容，回憶一下在學校念的一些寫程式的概念與架構。讓我們聊聊 radix sort 概念。

radix sort 理解基數排序方法

基於比較的排序算法（合併排序、堆排序、快速排序等）的下限是 Ω(nLogn)，即它們不能比nLogn 做得更好。計數排序是一種線性時間排序算法，當元素在從 1 到 k 的範圍內時，它在 O(n+k) 時間內排序。

如果元素在1 到 n 2的範圍內怎麼辦？

我們不能使用計數排序，因為計數排序需要 O(n 2 )，這比基於比較的排序算法更差。我們可以在線性時間內對這樣的數組進行排序嗎？

基數排序就是答案。基數排序的思想是從最低有效位到最高有效位進行逐位排序。基數排序使用計數排序作為子程序進行排序。

基數排序算法

對每個數字 i 執行以下操作，其中 i 從最低有效位到最高有效位變化。在這裡，我們將根據第 i 個數字使用計數排序（或任何穩定排序）對輸入數組進行排序。

例子：

原始未排序列表：170、45、75、90、802、24、2、66 按最低有效位（1 位）排序給出：[*注意我們將 802 保留在 2 之前，因為 802 在原始列表中出現在 2 之前, 對 170 & 90 和 45 & 75 類似。] 17 0 , 9 0 , 80 2 , 2 , 2 4 , 4 5 , 7 5 , 6 6按下一位（10 位）排序給出： [*注意802 再次出現在 2 之前，因為 802 在上一個列表中出現在 2 之前。] 8 0 2, 2, 2 4, 4 5, 6 6, 1 7 0, 7 5, 90 按最高有效數字（100位）排序給出： 2、24、45、66、75、90、1 70、8 02

Radix Sort 的運行時間是多少？

假設輸入整數中有 d 個數字。基數排序需要 O(d*(n+b)) 時間，其中 b 是表示數字的基數，例如，對於十進制系統，b 是 10。d 的值是多少？如果 k 是最大可能值，則 d 將為 O(log b (k))。所以整體時間複雜度是 O((n+b) * log b (k))。這看起來比基於比較的大 k 排序算法的時間複雜度要高。讓我們首先限制k。讓 k <= n c其中 c 是一個常數。在這種情況下，複雜度變為 O(nLog b (n))。但它仍然無法擊敗基於比較的排序算法。如果我們讓 b 的值更大呢？使時間複雜度線性化的 b 值應該是多少？如果我們將 b 設置為 n，我們得到的時間複雜度為 O(n)。換句話說，如果數字以 n 為底表示（或者每個數字佔用 log 2 (n) 位），我們可以對范圍從 1 到 n c的整數數組進行排序。

基數排序的應用：

在典型的計算機中，它是順序隨機存取機器，其中記錄由多個字段鍵控，基數排序被使用。例如，您想按月、日和年這三個鍵進行排序。您可以在年份比較兩條記錄，然後在月份比較並列，最後在日期比較。或者，可以使用基數排序對數據進行三次排序，首先按日期，然後按月份，最後按年份。
它用於有80列的卡片分揀機，並且在每列中，機器只能在12個位置打孔。然後分類器被編程為根據卡片被打孔的位置對卡片進行分類。然後，操作員使用它來收集第一排打孔的卡片，然後是第二排打孔的卡片，依此類推

基數排序比快速排序等基於比較的排序算法更可取嗎？

如果我們為每個數字設置 log 2 n 位，則 Radix 的運行時間似乎比快速排序對於大範圍的輸入數字要好。基數排序中隱藏在漸近符號中的常數因子更高，快速排序更有效地使用硬件緩存。此外，基數排序使用計數排序作為子程序，計數排序需要額外的空間來對數字進行排序。

基數排序的要點：

這裡給出了一些關於基數排序的關鍵點

它對數據做出假設，例如數據必須在一系列元素之間。
輸入數組必須具有相同基數和寬度的元素。
數排序基於單個數字或字母位置進行排序。
我們必須從最右邊的位置開始排序，並在每個位置使用穩定的算法。
基數排序不是就地算法，因為它使用臨時計數數組。

流程圖

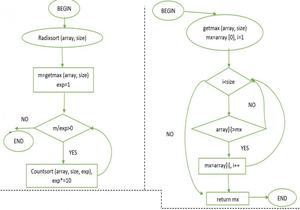
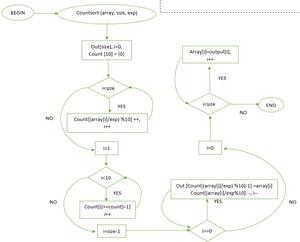
實現：基數排序

推薦實踐Radix Sort 試試看！

以下是基數排序的簡單實現。為簡單起見，假設 d 的值為 10。我們建議您查看以下代碼中有關 countSort() 函數的詳細信息的計數排序。

// C++ implementation of Radix Sort

#include
using namespace std;

// A utility function to get maximum value in arr[]
int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}

// A function to do counting sort of arr[] according to
// the digit represented by exp.
void countSort(int arr[], int n, int exp)
{
int output[n]; // output array
int i, count[10] = { 0 };

// Store count of occurrences in count[]
for (i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;

// Change count[i] so that count[i] now contains actual
// position of this digit in output[]
for (i = 1; i < 10; i++)
count[i] += count[i - 1];

// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}

// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current digit
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// The main function to that sorts arr[] of size n using
// Radix Sort
void radixsort(int arr[], int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);

// Do counting sort for every digit. Note that instead
// of passing digit number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}

// A utility function to print an array
void print(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}

// Driver Code
int main()
{
int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
int n = sizeof(arr) / sizeof(arr[0]);

// Function Call
radixsort(arr, n);
print(arr, n);
return 0;
}

輸出

2 24 45 66 75 90 170 802

以下是在使用桶排序技術時實現基數排序的另一種方式，看代碼時可能看起來並不簡單，但如果你試一試，它很容易，必須更深入地了解桶排序。

// implementation of radix sort using bin/bucket sort
#include
using namespace std;

// structure for a single linked list to help further in the
// sorting
struct node {
int data;
node* next;
};

// function for creating a new node in the linked list
struct node* create(int x)
{
node* temp = new node();
temp->data = x;
temp->next = NULL;

return temp;
}

// utility function to append node in the linked list
// here head is passed by reference, to know more about this
// search pass by reference
void insert(node*& head, int n)
{
if (head == NULL) {
head = create(n);
return;
}

node* t = head;
while (t->next != NULL)
t = t->next;
t->next = create(n);
}

// utility function to pop an element from front in the list
// for the sake of stability in sorting
int del(node*& head)
{
if (head == NULL)
return 0;
node* temp = head;
// storing the value of head before updating
int val = head->data;

// updation of head to next node
head = head->next;

delete temp;
return val;
}

// utility function to get the number of digits in the
// max_element
int digits(int n)
{
int i = 1;
if (n < 10)
return 1;

while (n > (int)pow(10, i))
i++;
return i;
}

void radix_sort(vector& arr)
{
// size of the array to be sorted
int sz = arr.size();

// getting the maximum element in the array
int max_val = *max_element(arr.begin(), arr.end());

// getting digits in the maximum element
int d = digits(max_val);

// creating buckets to store the pointers
node** bins;

// array of pointers to linked list of size 10 as
// integers are decimal numbers so they can hold numbers
// from 0-9 only, that's why size of 10

bins = new node*[10];

// initializing the hash array with null to all
for (int i = 0; i < 10; i++)
bins[i] = NULL;

// first loop working for a constant time only and inner
// loop is iterating through the array to store elements
// of array in the linked list by their digits value
for (int i = 0; i < d; i++) {
for (int j = 0; j < sz; j++) // bins updation
insert(bins[(arr[j] / (int)pow(10, i)) % 10],
arr[j]);

int x = 0, y = 0;
// write back to the array after each pass

while (x < 10) {
while (bins[x] != NULL)
arr[y++] = del(bins[x]);
x++;
}
}
}

// a utility function to print the sorted array
void print(vector arr)
{
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
cout << endl;
}
int main()
{
vector arr = { 573, 25, 415, 12, 161, 6 };

// function call
radix_sort(arr);
print(arr);

return 0;
}